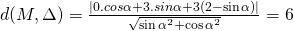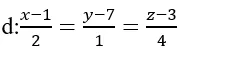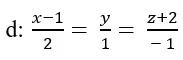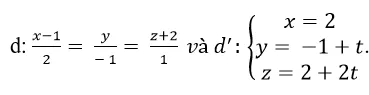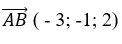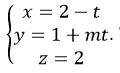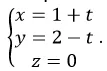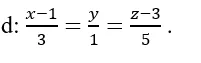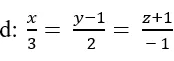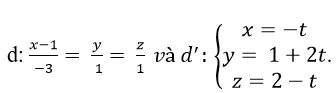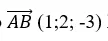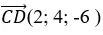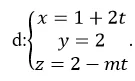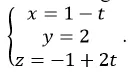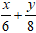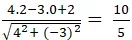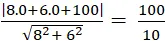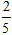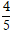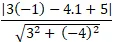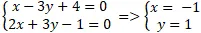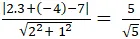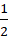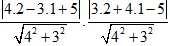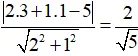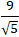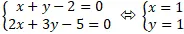Công thức tính khoảng cách từ điểm đến đường thẳng trong không gian – Kiến Thức Cho Người lao Động Việt Nam
Khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian
Khoảng cách từ 1 điểm đến 1 đường thẳng trong khoảng trống được tính thế nào ? Bài viết dưới đây hướng dẫn các em 2 cách để tính khoảng cách từ 1 điểm đến đường thẳng. Các em cùng theo dõi nhé ! Nội Dung
-
1
Bạn đang đọc: Công thức tính khoảng cách từ điểm đến đường thẳng trong không gian
Bạn đang đọc: Công thức tính khoảng cách từ điểm đến đường thẳng trong không gian – Kiến Thức Cho Người lao Động Việt Nam
KHOẢNG CÁCH TỪ ĐIỂM ĐẾN 1 ĐƯỜNG THẲNG TRONG KHÔNG GIAN
- 2 CÔNG THỨC TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN 1 ĐƯỜNG THẲNG TRONG KHÔNG GIAN OXYZ
- 2.1 1. TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN 1 ĐƯỜNG THẲNG TRONG OXYZ BẰNG CÁCH TÌM HÌNH CHIẾU
- 2.2 2. TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN ĐƯỜNG THẲNG TRONG OXYZ BẰNG TÍCH CÓ HƯỚNG
Trong hình học mặt phẳng Oxy lớp 10 và hình học không gian Oxyz lớp 12 đều có dạng toán tìm khoảng cách từ điểm tới đường thẳng Δ cho trước. Đây là dạng toán tương đối đơn giản, bạn chỉ cần nhớ chính xác công thức là làm tốt. Nếu bạn quên có thể xem lại lý thuyết bên dưới, đi kèm với nó là bài tập có lời giải chi tiết tương ứng
Đánh Giá khoảng cách 1 điểm đến đường thẳng
Đánh Giá – 9.3
Đánh Giá – 9.7
9.5
100
Hướng dẫn khoảng cách từ 1 điểm đến 1 đường thẳng oke ạ !
User Rating: 4.65 ( 1 votes)
Trong hình học không gian Oxyz thường có dạng toán tìm khoảng cách từ điểm đến đường thẳng cho trước. Đây là một dạng toán khá đơn giản và phổ biến mà chỉ cần nhớ chính xác công thức và áp dụng vào giải toán dễ dàng. Hãy theo dõi bài viết này để tìm hiểu công thức tính khoảng cách từ 1 điểm đến đường thẳng nhé! Hãy tìm hiểu dưới đây với Mobitool nhé !
Video hướng dẫn tính khoảng cách từ một điểm đến đường thẳng
Hướng dẫn công thức khoảng cách từ điểm đến đường thẳng
Hãy khám phá thêm công thức khoảng cách từ điểm đến đường thẳng mới nhất dưới đây :
1. Điểm là gì?
Điểm trong khái niệm toán học đơn thuần được thừa nhận như một khái niệm xuất phát để phong cách thiết kế kiến thiết xây dựng môn hình học, được tưởng tượng là một thứ rất nhỏ bé, không có kích cỡ hay size bằng không .
2. Đường thẳng là gì?
Đường thẳng là một đường dài vô hạn, mỏng mảnh vô cùng và thẳng tuyệt đối .
3. Khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian là gì?
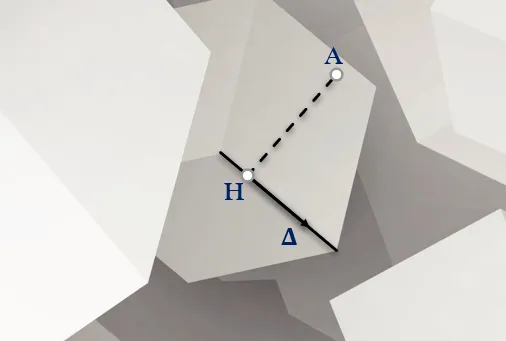
Trong khoảng trống cho điểm A và đường thẳng Δ bất kể. Gọi điểm B là hình chiếu của điểm A lên đường thẳng Δ. Khi đó độ dài đoạn thẳng AB chính là khoảng cách từ điểm A lên đường thẳng Δ .
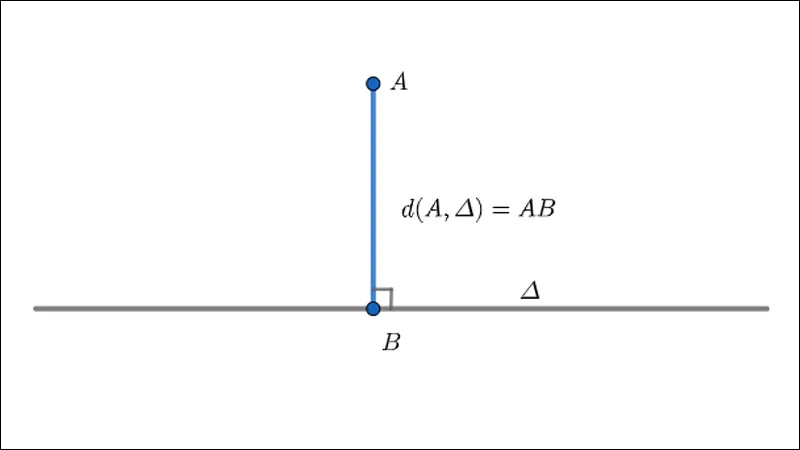
Khoảng cách từ điểm đến đường thẳng trong khoảng trống Nói cách khác, khoảng cách từ điểm đến đường thẳng trong khoảng trống là khoảng cách giữa điểm và hình chiếu của nó trên đường thẳng. Ký hiệu là d ( A, Δ ) .
4. Công thức tính khoảng cách từ một điểm đến đường thẳng
Công thức tính khoảng cách từ điểm đến đường thẳng
5. Cách tính khoảng cách từ điểm đến đường thẳng bằng tích có hướng
Cách tính khoảng cách từ điểm đến đường thẳng bằng tích có hướng
Ví dụ:
Ví dụ về tính khoảng cách từ điểm đến đường thẳng bằng tích có hướng
Lời giải:
Lời giải của ví dụ trên
6. Cách tính khoảng cách giữa 2 điểm
Cách tính khoảng cách giữa 2 điểm
Ví dụ: Trong mặt phẳng Oxy, cho điểm A (1;2) và điểm B(-3;4). Tính độ dài đoạn thẳng AB.
Lời giải:
Lời giải của ví dụ trên
7. Bài tập tính khoảng cách từ một điểm đến một đường thẳng
Bài 1: Cho một đường thẳng có phương trình có dạng Δ: – x + 3y + 1 = 0. Hãy tính khoảng cách từ điểm Q (2;1) tới đường thẳng Δ.
Lời giải:
Lời giải của bài tập 1
Bài 2:
Bài tập 2
Lời giải:
Lời giải của bài tập 2
Bài 3:
Bài tập 3
Lời giải:
Lời giải của bài tập 3
Bài 4: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng (d): 8x + 6y + 100 = 0. Tính bán kính R của đường tròn (C).
Lời giải:
Lời giải của bài tập 4
Bài 5: Tính Khoảng cách từ giao điểm của hai đường thẳng (a): x – 3y + 4 = 0 và (b): 2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0.
Lời giải:
Lời giải của bài tập 5
Bài 6: Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4) .Tính diện tích tam giác ABC?
Lời giải:
Lời giải của bài tập 6
Bài 7:
Bài tập 7
Lời giải:
Lời giải của bài tập 7
8. Một số lưu ý về tính khoảng cách từ điểm đến đường thẳng
– Cần xác lập được khái niệm khoảng cách từ điểm đến đường thẳng là như thế nào. – Đưa phương trình đường thẳng về dạng tổng quát trước khi vận dụng công thức tính khoảng cách từ điểm đến đường thẳng. – Nên sử dụng máy tính cầm tay để trọn vẹn hoàn toàn có thể tương hỗ tính khoảng cách từ điểm đến đường thẳng một cách nhanh gọn và đúng chuẩn nhất .
Sử dụng máy tính cầm tay để tính khoảng cách từ điểm đến đường thẳng nhanh gọn Xem thêm : Hướng dẫn lim căn bậc n của n Từ khóa tìm kiếm : khoảng cách từ điểm tới đường thẳng, công thức tính khoảng cách từ một điểm đến đường thẳng, công thức tính khoảng cách điểm đến đường thẳng, công thức tính khoảng cách từ 1 điểm đến 1 đường thẳng, công thức tính khoảng cách từ một điểm đến một đường thẳng, khoảng cách từ điểm đến đường thẳng oxyz, công thức tính khoảng cách giữa điểm và đường thẳng, tìm khoảng cách từ điểm đến đường thẳng, cách xác lập khoảng cách từ 1 điểm đến đường thẳng, công thức khoảng cách từ 1 điểm đến 1 đường thẳng, cách tính khoảng cách từ 1 điểm đến 1 đường thẳng, tính khoảng cách từ một điểm đến đường thẳng, tính khoảng cách điểm đến đường thẳng, tìm khoảng cách từ 1 điểm đến đường thẳng, khoảng cách từ 1 điểm đến 1 đường thẳng là gì, khoảng cách một điểm đến đường thẳng, khoảng cách 1 điểm đến 1 đường thẳng, khoảng cách từ một điểm đến một đường thẳng trong khoảng trống, công thức khoảng cách, khoảng cách 1 điểm đến đường thẳng oxyz, khoảng cách điểm đến đường thẳng oxyz, cách tính khoảng cách từ một điểm đến một đường thẳng, công thức tính khoảng cách 1 điểm đến đường thẳng, tính khoảng cách giữa điểm và đường thẳng, ct tính khoảng cách từ điểm đến đường thẳng, khoảng cách từ 1 điểm đến 1 đường thẳng trong oxyz, khoảng cách từ tâm đến đường thẳng, khoảng cách giữa 1 điểm và 1 đường thẳng, tính khoảng cách 1 điểm đến đường thẳng, khoảng cách từ 1 điểm đến đường thẳng trong oxyz, khoang cach tu diem den duong thang, khoảng cách giữa 1 điểm và đường thẳng, khoảng cách từ điểm đến đoạn thẳng, công thức khoảng cách điểm đến đường thẳng, công thức từ điểm đến đường thẳng, khoảng cách từ 1 điểm đến 1 đường thẳng trong oxy, gọi khoảng cách từ điểm i đến đường thẳng a là d, khoảng cahcs từ điểm đến đường thẳng, công thức tính độ dài từ điểm đến đường thẳng, công thức tính khoảng cách từ tâm đến đường thẳng, khoảng cách từ 1 điểm tới 1 đường thẳng, công thức tính khoảng cách từ điểm đến đường thẳng trong khoảng trống, khoảng cách từ điểm tới đường, cách tính khoảng cách từ một điểm đến đường thẳng, khoảng cách điểm tới đường thẳng, khoảng cách ký hiệu là gì, khoảng cách từ 1 điểm đến dường thẳng, kc từ điểm đến đt, khoảng cách từ một điểm tới một đường thẳng, công thức từ 1 điểm đến đường thẳng, khoảng cách từ điểm đến đường thẳng trong hệ oxyz, công thức tính khoảng cách từ 1 điểm đến đt, tính độ dài từ 1 điểm đến đường thẳng, khoảng cách từ 1 điểm đến 1 đoạn thẳng, công thức tính khoảng cách từ điểm tới đường thẳng, khoảng cách từ điểm đến một đường thẳng, tính khoảng cách từ điểm tới đường thẳng, khoang cach tu 1 diem den 1 duong thang, độ dài từ 1 điểm đến 1 đường thẳng, khoảng cách từ một điểm đến một đường thẳng là gì, tính khoảng cách giữa 1 điểm đến đường thẳng, phương trình khoảng cách, công thức tính khoảng cách d, khoảng cách từ từ, khoảng cách từ một điểm đến một đoạn thẳng, khoảng cách từ điểm đến đường thẳng oxy, khoảng cách từ một điểm đến 1 đường thẳng, tính khoảng cách d, tính khoảng cách từ điểm đến đoạn thẳng, công thức tiính khoảng cách, khoảng cách điểm và đường thẳng, công thức tính khoảng cách r, khoảng cách từ 1 điểm đến 1 vecto, tính khoảng cách trong khoảng trống oxyz, Tagscách tính khoảng cách từ 1 điểm đến 1 đường thẳng cách xác lập khoảng cách từ 1 điểm đến đường thẳng công thức khoảng cách từ 1 điểm đến 1 đường thẳng công thức tính khoảng cách điểm đến đường thẳng công thức tính khoảng cách giữa điểm và đường thẳng công thức tính khoảng cách từ 1 điểm đến 1 đường thẳng công thức tính khoảng cách từ một điểm đến đường thẳng công thức tính khoảng cách từ một điểm đến một đường thẳng Đời sống Hỏi đáp khoảng cách từ điểm đến đường thẳng oxyz khoảng cách từ điểm tới đường thẳng tìm khoảng cách từ điểm đến đường thẳng Wiki – Thuật ngữ
Khoảng cách từ 1 điểm đến 1 đường thẳng trong oxy
Cho đường thẳng Delta :
và điểm M0 ( x0, y0 ). Khoảng cách từ điểm đến đường thẳng được tính theo công thức :
Ví dụ :
Tính khoảng cách từ điểm 
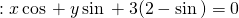
Lời giải :
Khoảng cách từ điểm 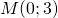 đến đường thẳng
đến đường thẳng 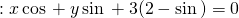 là:
là:
1. Khoảng cách từ 1 điểm đến 1 đường thẳng trong mặt phẳng Oxy
Nếu biết phương trình đường thẳng d : ax + by + c = 0 và tọa độ điểm A ( x0 ; y0 ) thì khoảng cách từ điểm A tới đường thẳng d được xác lập theo công thứcUSD d \ left ( { M, d } \ right ) = \ frac { { \ left | { a { x_0 } + b { y_0 } + c } \ right | } } { { \ sqrt { { a ^ 2 } + { b ^ 2 } } } } $
Ví dụ: Trong hệ trục tọa độ Oxy, bạn hãy tính khoảng cách từ điểm M tới đường thẳng d, biết:
a ) M ( 3 ; 4 ) và x + y – 6 = 0 b ) M ( – 4 ; 2 ) và 2 x + y + 1 = 0 c ) M ( 2 ; 7 ) và 5 x – 6 x + 11 = 0L ời giảiKhi đã biết tọa độ và phương trình đường thẳng, ta vận dụng công thức ở trên : USD d \ left ( { M, d } \ right ) = \ frac { { \ left | { a { x_0 } + b { y_0 } + c } \ right | } } { { \ sqrt { { a ^ 2 } + { b ^ 2 } } } } $ a ) USD d \ left ( { M, d } \ right ) = \ frac { { \ left | { 1.3 + 1.4 – 6 } \ right | } } { { \ sqrt { { 1 ^ 2 } + { 1 ^ 2 } } } } = \ frac { { \ sqrt 2 } } { 2 } $ b ) USD d \ left ( { M, d } \ right ) = \ frac { { \ left | { 2. \ left ( { – 4 } \ right ) + 1.2 + 1 } \ right | } } { { \ sqrt { { 2 ^ 2 } + { 1 ^ 2 } } } } = \ sqrt 5 USDc ) USD d \ left ( { M, d } \ right ) = \ frac { { \ left | { 5.2 + \ left ( { – 6 } \ right ). 7 + 11 } \ right | } } { { \ sqrt { { 5 ^ 2 } + { { \ left ( { – 6 } \ right ) } ^ 2 } } } } \ approx 2,69 $
Khoảng cách từ 1 điểm đến 1 đường thẳng; Khoảng cách giữa 2 đường thẳng chéo nhau
Trang trước Trang sau
Bài giảng: Các dạng bài về khoảng cách, góc trong không gian – Cô Nguyễn Phương Anh (Giáo viên Tôi)
Quảng cáo
– Muốn tìm khoảng cách từ một điểm M đến đường thẳng d : có 2 cách sau :
+ Cách 1 : Tìm hình chiếu H của điểm đó đến d => MH là khoảng cách từ A đến d
+ Cách 2. công thức ( với u → là vectơ chỉ phương của d và M0 là một điểm thuộc d )
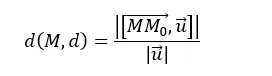
– Muốn tìm khoảng cách giữa hai đường thẳng chéo nhau d ( u → là vectơ chỉ phương của d và d đi qua M0 ) và d ’ ( ( u ‘ ) ⃗ là vectơ chỉ phương của d ’ và d ’ đi qua M0 ‘ ) ta làm như sau :
+ Viết phương trình mặt phẳng ( P ) chứa d và song song d ’
+ Khoảng cách giữa d và d ’ chính là khoảng cách từ điểm M0 ‘ đến mặt phẳng ( P ) d ( d, d ’ ) = d ( M0 ‘, ( P ) )
+ Hoặc dùng công thức :
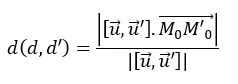
Ví dụ: 1
Tìm khoảng cách của A(-2; 1; 3) đến đường thẳng 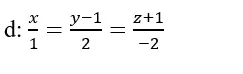
A. 
B. 
C. 2
D. 
Quảng cáo
Hướng dẫn giải
Đường thẳng d đi qua B(0;1; -1) và có vectơ chỉ phương 
Ta có: 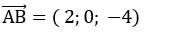
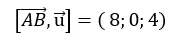
Vậy
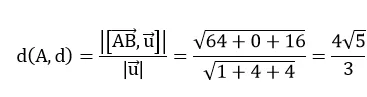
Chọn B .
Ví dụ: 2
Cho mặt phẳng (P): 3x – 2y – z + 5 = 0 và đường thẳng
Tính khoảng cách giữa d và ( P. )
A. 
B. 
C. 
D. 
Hướng dẫn giải
Mặt phẳng (P) có vecto pháp tuyến 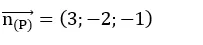
Đường thẳng d có vecto chỉ phương
và đi qua điểm M0(1;7;3)
Ta có: 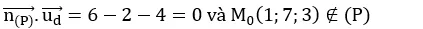
Vậy d / / ( P. )
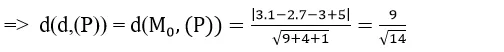
Chọn D .
Ví dụ: 3
Tính khoảng cách giữa hai đường thẳng
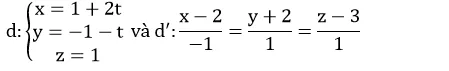
A. 
B. 
C. 
D. 1
Hướng dẫn giải
Cách 1 :
Đường thẳng d có vecto chỉ phương là: 
Đường thẳng d’ có vecto chỉ phương là:
.
– Gọi ( P. ) là mặt phẳng chứa d và song song với d ’. ( P. ) nhận vectơ pháp tuyến là
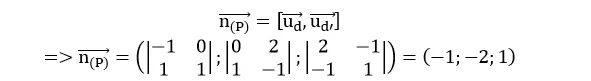
M0 ( 1 ; – 1 ; 1 ) thuộc d cũng thuộc ( P ) nên phương trình mặt phẳng ( P ) là :
– 1 ( x-1 ) – 2 ( y + 1 ) + 1 ( z-1 ) = 0 hay x + 2 y – z + 2 = 0
– d ’ đi qua M0 ‘ ( 2 ; – 2 ; 3 )
Vậy 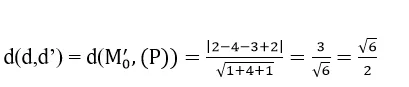
Cách 2 :
Ta có :
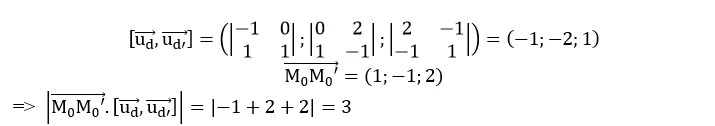
Vậy
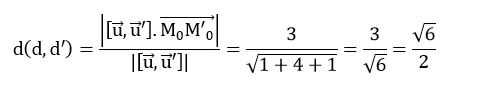
chọn A.
Quảng cáo
Ví dụ: 4
Trong không gian với hệ tọa độ Oxyz; cho đường thẳng
và điểm A( -1; 2; 1). Tính khoảng cách từ điểm A đến đường thẳng d?
A.
B. 
C. 
D. Đáp án khác
Hướng dẫn giải
+ Đường thẳng d đi qua điểm M( 1; 0; – 2) và có vecto chỉ phương 
+ Ta có: 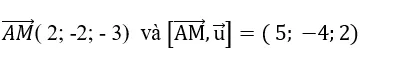
=> Khoảng cách từ A đến đường thẳng d là :
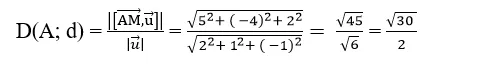
Chọn C .
Ví dụ: 5
Trong khoảng trống với hệ tọa độ Oxyz ; cho hai đường thẳng
. Xác định khoảng cách giữa hai đường thẳng đã
cho ?
A. 
B.
C.
D. Tất cả sai
Hướng dẫn giải
+ Đường thẳng d đi qua A( 1;0; – 2) và có vecto chỉ phương 
+ Đường thẳng d’ đi qua B( 2; -1; 2) và có vecto chỉ phương 
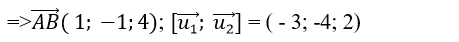
=> Khoảng cách giữa hai đường thẳng đã cho là :
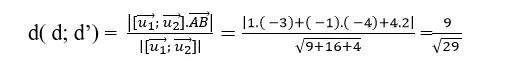
Chọn B .
Ví dụ: 6
Trong khoảng trống với hệ tọa độ Oxyz ; cho 3 điểm A ( 0 ; 1 ; 2 ) ; B ( – 2 ; 0 ; 1 ) và C ( 2 ; 1 ; – 3 ). Tính khoảng cách từ điểm A đến đường thẳng BC ?
A.
B.
C. 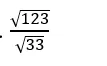
D. Đáp án khác
Hướng dẫn giải
+ Đường thẳng BC đi qua B( -2; 0;1) và nhận vecto
làm vecto chỉ phương
+ Ta có: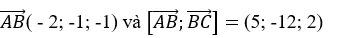
=> Khoảng cách từ điể A đến đường thẳng BC là :
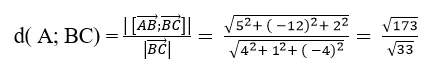
Chọn A .
Ví dụ: 7
Trong khoảng trống với hệ tọa độ Oxyz ; cho bốn điểm A ( 1 ; 2 ; – 1 ) ; B ( – 2 ; 1 ; 1 ) C ( 2 ; 1 ; 3 ) và D ( – 1 ; 0 ; 5 ). Tính khoảng cách hai đường thẳng AB và CD ? biết rằng ba điểm A, C và D không thẳng hàng .
A. 
B. 
C. 
D. 
Hướng dẫn giải
+ Đường thẳng AB: đi qua A(1;2; -1) và nhận vecto
làm vecto chỉ phương
+ Đường thẳng CD đi qua C( 2; 1; 3) và nhận vecto
làm vecto chỉ phương.
+ Hai đường thẳng AB và CD có cùng vecto chỉ phương và điểm A không thuộc đường thẳng CD .
=> AB / / CD nên d ( AB ; CD ) = d ( A ; CD )
+ Ta có: 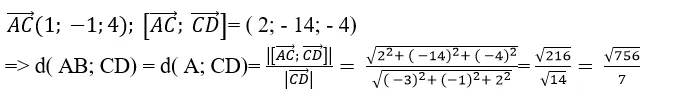
Chọn C .
Ví dụ: 8
Trong không gian với hệ tọa độ Oxyz; cho điểm A(-1; 0;2) và đường thẳng d:
. Tìm m để khoảng cách từ A đến d là
?
A. m = – 1 hoặc m = ( – 2 ) / 3
B. m = – 1 hoặc m = 1/7
C. m = 1 hoặc m = – 1
D. m = 1 hoặc m = 1/7
Hướng dẫn giải
+ Đường thẳng d đi qua M( 2; 1; 2) và có vecto chỉ phương 
+ Ta có; 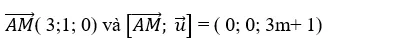
+ Theo đầu bài ta có: d( A; d)= 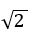
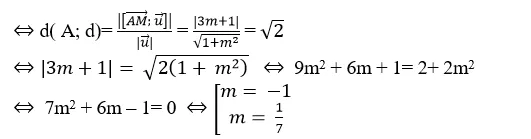
Chọn B .
Ví dụ: 9
Trong không gian với hệ tọa độ Oxyz; cho điểm A( 1; m;2) và đường thẳng
. Tìm m để khoảng cách từ A đến đường thẳng d là 2?
A. m = 2
B. m = – 1
C. m = 3
D. m = – 4
Hướng dẫn giải
+ Đường thẳng d đi qua M( 1; 2; 0) và có vecto chỉ phương 
+ Ta có: 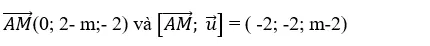
+ Để khoảng cách từ A đến d là 2 thì :
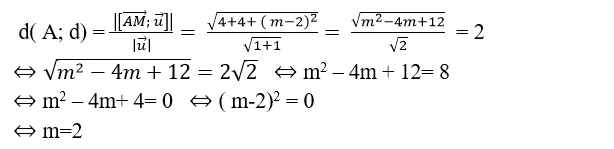
Chọn A .
Câu 1:
Tìm khoảng cách của A( 1;-2; 1) đến đường thẳng 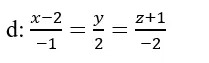
A. 
B. 
C. 2
D. 
Hiển thị lời giải
Đường thẳng d đi qua B(2;0; -1) và có vectơ chỉ phương 
Ta có: 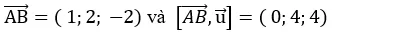
Vậy
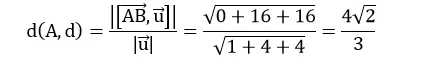
Chọn B .
Câu 2:
Cho mặt phẳng (P): x + 2y – z + 1= 0 và đường thẳng
.
Tính khoảng cách giữa d và (P)
A.
B.
C.
D. 
Hiển thị lời giải
Mặt phẳng (P) có vecto pháp tuyến 
Đường thẳng d có vecto chỉ phương
và đi qua điểm M0 (1;0;3)
Ta có: 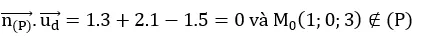
Vậy d / / ( P )
Xem thêm: So sánh ẩm thực Trung Quốc và Việt Nam
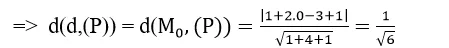
Chọn C .
Câu 3:
Tính khoảng cách giữa hai đường thẳng
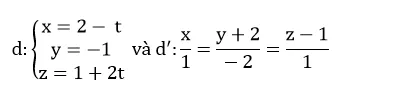
A. 
B. 
C.
D. 
Hiển thị lời giải
Đường thẳng d đi qua A( 2; -1; 1) và có vecto chỉ phương
.
Đường thẳng d’ đi qua B( 0; -2; 1) và có vecto chỉ phương 
Ta có: 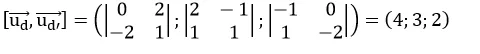
Và 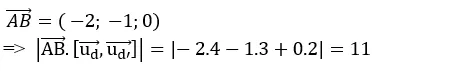
Vậy
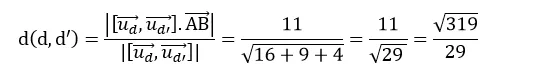
Chọn D .
Câu 4:
Trong không gian với hệ tọa độ Oxyz; cho đường thẳng
và điểm A( 0;-2; 3). Tính khoảng cách từ điểm A đến đường thẳng d?
A. 
B.
C. 
D. Đáp án khác
Hiển thị lời giải
+ Đường thẳng d đi qua điểm M( 0;1; -1) và có vecto chỉ phương 
+ Ta có; 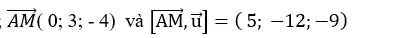
=> Khoảng cách từ A đến đường thẳng d là :
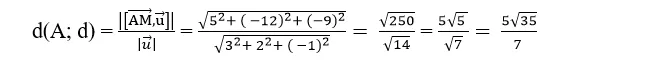
Chọn A .
Câu 5:
Trong khoảng trống với hệ tọa độ Oxyz ; cho hai đường thẳng
. Xác định khoảng cách giữa hai đường thẳng đã
cho ?
A. 
B. 
C. 
D. Tất cả sai
Hiển thị lời giải
+ Đường thẳng d đi qua A( 1;0; 0) và có vecto chỉ phương 
+ Đường thẳng d’ đi qua B(0;1; 2) và có vecto chỉ phương 
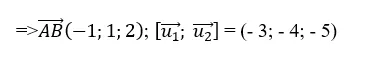
=> Khoảng cách giữa hai đường thẳng đã cho là :
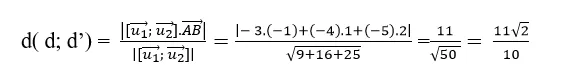
Chọn D .
Câu 6:
Trong khoảng trống với hệ tọa độ Oxyz ; cho hai điểm A ( 2 ; – 1 ; – 1 ) ; B ( 2 ; 3 ; 1 ). Tính khoảng cách từ điểm O đến đường thẳng AB ?
A.
B. 
C. 
D. Đáp án khác
Hiển thị lời giải
+ Đường thẳng AB đi qua A( 2; -1; -1) và nhận vecto
làm vecto chỉ phương
+ Ta có: 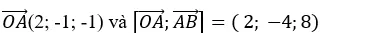
=> Khoảng cách từ điểm O đến đường thẳng AB là :
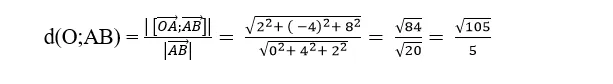
Chọn A .
Câu 7:
Trong khoảng trống với hệ tọa độ Oxyz ; cho bốn điểm A ( 0 ; 0 ; 2 ) ; B ( 1 ; 2 ; – 1 ) C ( 2 ; 1 ; 3 ) và D ( 4 ; 5 ; – 3 ). Tính khoảng cách hai đường thẳng AB và CD ? biết rằng ba điểm A, C và D không thẳng hàng .
A. 
B. 
C.
D. 
Hiển thị lời giải
+ Đường thẳng AB: đi qua A(0;0; 2) và nhận vecto
làm vecto chỉ phương
+ Đường thẳng CD đi qua C( 2; 1; 3) và nhận vecto
làm vecto chỉ phương.
+ Hai đường thẳng AB và CD có hai vecto chỉ phương là cùng phương và điểm A không thuộc đường thẳng CD .
=> AB / / CD nên d ( AB ; CD ) = d ( A ; CD )
+ Ta có: 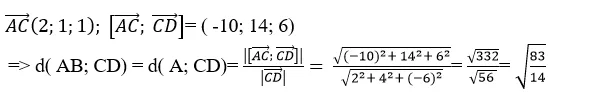
Chọn C .
Câu 8:
Trong khoảng trống với hệ tọa độ Oxyz ; cho điểm A ( 1 ; 1 ; 1 ) và đường thẳng
. Tìm m để khoảng cách từ A đến d là
?
A. m = – 1
B. m = 0
C. m = – 2
D. m = 1
Hiển thị lời giải
+ Đường thẳng d đi qua M( 1;2; 2) và có vecto chỉ phương 
+ Ta có; 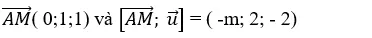
+ Theo đầu bài ta có: d( A; d)= 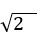
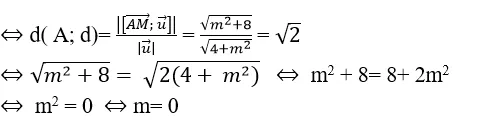
Chọn B .
Câu 9:
Trong không gian với hệ tọa độ Oxyz; cho điểm A(m; 0; 2) và đường thẳng
. Tìm m để khoảng cách từ A đến đường thẳng d là
?
A. m = 2 hoặc m = 1
B. m = – 1 hoặc m = 0
C. m = 3 hoặc m = 0
D. m = – 4 hoặc m = – 1
Hiển thị lời giải
+ Đường thẳng d đi qua M( 1; 2; – 1) và có vecto chỉ phương 
+ Ta có: 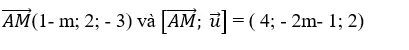
+ Để khoảng cách từ A đến d là 2 thì :
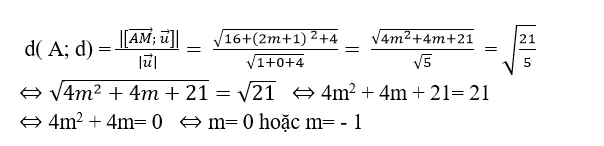
Chọn B .
Bài giảng: Các dạng bài về khoảng cách, góc trong không gian – Cô Nguyễn Phương Anh (Giáo viên Tôi)
Xem thêm các chuyên đề Toán lớp 12 có trong đề thi THPT Quốc gia khác :
Giới thiệu kênh Youtube Tôi
Trang trước Trang sau
Tính khoảng cách từ một điểm đến một đường thẳng
Trang trước Trang sau
Quảng cáo
+ Cho đường thẳng d: ax + by + c = 0 và điểm M ( x0; y0). Khi đó khoảng cách từ điểm
M đến đường thẳng d là: d(M; d) = 
+ Cho điểm A ( xA ; yA ) và điểm B ( xB ; yB ). Khoảng cách hai điểm này là :
AB = 
Chú ý: Trong trường hợp đường thẳng d chưa viết dưới dạng tổng quát thì đầu tiên ta cần đưa đường thẳng d về dạng tổng quát.
Ví dụ 1: Khoảng cách từ điểm M( 1; -1) đến đường thẳng ( a) : 3x – 4y – 21 = 0 là:
A. 1
B. 2
C.
D. 
Hướng dẫn giải
Khoảng cách từ điểm M đến đường thẳng ( a ) là :
d(M;a) =
= 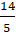
Chọn D.
Ví dụ 2: Khoảng cách từ điểm O đến đường thẳng d:
= 1 là:
A. 4,8
B.
C. 1
D. 6
Hướng dẫn giải
Đường thẳng d:
= 1 ⇔ 8x + 6y – 48 = 0
⇒ Khoảng cách từ điểm O đến đường thẳng d là :
d( O; d) =
= 4,8
Chọn A.
Quảng cáo
Ví dụ 3: Khoảng cách từ điểm M(2; 0) đến đường thẳng
là:
A. 2
B.
C.
D. 
Hướng dẫn giải
+ Ta đưa đường thẳng d về dạng tổng quát :
(d) : 
⇒ Phương trình ( d ) : 4 ( x – 1 ) – 3 ( y – 2 ) = 0 hay 4 x – 3 y + 2 = 0 + Khoảng cách từ điểm M đến d là :
d( M; d) =
= 2
Chọn A.
Ví dụ 4. Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng
(d): 8x + 6y + 100 = 0. Bán kính R của đường tròn (C) bằng:
A. R = 4
B. R = 6
C. R = 8
D. R = 10
Lời giải
Do đường thẳng d tiếp xúc với đường tròn ( C ) nên khoảng cách từ tâm đường tròn đến đường thẳng d chính là nửa đường kính R của đường tròn
⇒ R= d(O; d) =
= 10
Chọn D.
Ví dụ 5 . Khoảng cách từ điểm M( -1; 1) đến đường thẳng d: 3x – 4y + 5 = 0 bằng:
A.
B. 1
C.
D. 
Lời giải
Khoảng cách từ điểm M đến đường thẳng d là :
d( M; d) =
=
Chọn A.
Quảng cáo
Ví dụ 6. Khoảng cách từ giao điểm của hai đường thẳng (a): x – 3y + 4 = 0 và
(b):
2x + 3y – 1 = 0 đến đường thẳng ∆: 3x + y + 16 = 0 bằng:
A. 2√10
B.
C.
D. 2
Lời giải
Gọi A là giao điểm của hai đường thẳng ( a ) và ( b ) tọa độ điểm A là nghiệm hệ phương trình :
⇒ A( -1; 1)
Khoảng cách từ điểm A đến đường thẳng ∆ là :
d( A; ∆) =
= 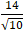
Chọn C
Ví dụ 7. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A( 1; 2) ; B(0; 3) và C(4; 0). Chiều cao của tam giác kẻ từ đỉnh A bằng:
A.
B. 3
C.
D. 
Lời giải
+ Phương trình đường thẳng BC :
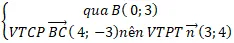
⇒ ( BC ) : 3 ( x – 0 ) + 4 ( y – 3 ) = 0 hay 3 x + 4 y – 12 = 0 ⇒ chiều cao của tam giác kẻ từ đỉnh A chính là khoảng cách từ điểm A đến đường thẳng BC .
d( A; BC) =
= 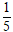
Chọn A.
Ví dụ 8. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3; -4); B(1; 5) và C(3;1). Tính diện tích tam giác ABC.
A. 10
B. 5
C. √26
D. 2√5
Lời giải
+ Phương trình BC :
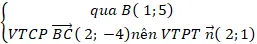
⇒ Phương trình BC : 2 ( x – 1 ) + 1 ( y – 5 ) = 0 hay 2 x + y – 7 = 0
⇒ d( A;BC) =
= √5
+ BC =
= 2√5
⇒ diện tích tam giác ABC là: S =
.d( A; BC).BC =
.√5.2√5 = 5
Chọn B.
Ví dụ 9: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng d1 : 4x – 3y + 5 = 0 và
d2: 3x + 4y – 5 = 0, đỉnh A( 2; 1). Diện tích của hình chữ nhật là:
A. 1.
B. 2
C. 3
D. 4
Lời giải
+ Nhận xét : điểm A không thuộc hai đường thẳng trên. ⇒ Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A ( 2 ; 1 ) đến hai đường thẳng trên, do đó diện tích quy hoạnh quy hoạnh hình chữ nhật bằng
S =
= 2 .
Chọn B.
Câu 1: Khoảng cách từ điểm M( 2;0) đến đường thẳng
là:
A. 2
B.
C.
D. 
Hiển thị lời giải
Đáp án: A
Trả lời:
+ Ta đưa đường thẳng d về dạng tổng quát :
(d) : 
=> Phương trình ( d ) : 4 ( x – 1 ) – 3 ( y – 2 ) = 0 hay 4 x – 3 y + 2 = 0. + Khi đó khoảng cách từ M đến d là :
d(M, d)=
= 2
Câu 2: Đường tròn ( C) có tâm I ( -2; -2) và tiếp xúc với đường thẳng
d: 5x + 12y – 10 = 0. Bán kính R của đường tròn ( C) bằng:
A. R =
B. R =
C. R = 44
D. R = 
Hiển thị lời giải
Đáp án: A
Trả lời:
Do đường thẳng d tiếp xúc với đường tròn ( C ) nên khoảng cách từ tâm đường tròn ( C ) đến đường thẳng d chính là nửa đường kính đường tròn .
=> R = d(I; d) =
= 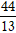
Câu 3: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a) : 4x – 3y + 5 = 0
và
(b) : 3x + 4y – 5 = 0. Biết hình chữ nhật có đỉnh A( 2 ;1). Diện tích của hình chữ nhật là:
A. 1
B. 2
C. 3
D. 4
Hiển thị lời giải
Đáp án: B
Trả lời:
Ta thấy : điểm A không thuộc hai đường thẳng trên. Độ dài hai cạnh kề của hình chữ nhật bằng khoảng cách từ A đến hai đường thẳng trên .
Độ dài 2 cạnh là: d( A; a) =
= 2; d(A; b) =
= 1
do đó diện tích quy hoạnh quy hoạnh hình chữ nhật bằng : S = 2.1 = 2
Câu 4: Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4) .Tính diện tích tam giác ABC ?
A. 3
B.
C.
D. 147
Hiển thị lời giải
Đáp án: A
Trả lời:
+ Phương trình đường thẳng AC: 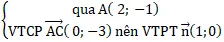
=> Phương trình AC : 1 ( x – 2 ) + 0. ( y + 1 ) = 0 hay x – 2 = 0 ..
+ Độ dài AC =
= 3 và khoảng cách từ B đến AC là:
d(B; AC) =
= 2
=> Diện tích tam giác ABC là : S = AC.d ( B ; AC ) =. 3.2 = 3 .
Câu 5: Khoảng cách từ A(3; 1) đến đường thẳng
gần với số nào sau đây ?
A. 0, 85
B. 0,9
C. 0,95
D. 1
Hiển thị lời giải
Đáp án: B
Trả lời:
Ta đưa đường thẳng d về dạng tổng quát :
(d): 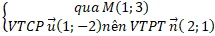
=> ( d ) : 2 ( x – 1 ) + 1 ( y – 3 ) = 0 hay 2 x + y – 5 = 0
=> d(A, d) =
≈ 0,894
Câu 6: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng 4x – 3y + 5 = 0 và
3x + 4y + 5 = 0
đỉnh A(2; 1). Diện tích của hình chữ nhật là
A. 6
B. 2
C. 3
D. 4
Hiển thị lời giải
Đáp án: A
Trả lời:
+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 4x – 3y + 5 = 0 là
= 2
+ Khoảng cách từ đỉnh A(2; 1) đến đường thẳng 3x + 4y + 5 = 0 là
= 3
=> Diện tích hình chữ nhật bằng 2.3 = 6
Câu 7: Tính diện tích hình bình hành ABCD biết A( 1; -2) ; B( 2; 0) và D( -1; 3)
A. 6
B. 4,5
C. 3
D. 9
Hiển thị lời giải
Đáp án: D
Trả lời:
+ Đường thẳng AB: 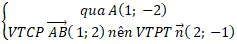
=> Phương trình AB : 2 ( x – 1 ) – 1 ( y + 2 ) = 0 hay 2 x – y – 4 = 0
+ độ dài đoạn AB: AB =
= √5
Khoảng cách từ D đến AB: d( D; AB)=
= 
=> Diện tích hình chữ nhật ABCD là S = AB.d( D; AB) = √5.
= 9
Câu 8: Tính khoảng cách từ giao điểm của hai đường thẳn (d) : x + y – 2 = 0 và
( ∆) : 2x + 3y – 5 = 0 đến đường thẳng (d’) : 3x – 4y + 11 = 0
A. 1
B. 2
C. 3
D. 4
Hiển thị lời giải
Đáp án: B
Trả lời:
+ Giao điểm A của hai đường thẳng d và ∆ là nghiệm hệ phương trình
=> A( 1; 1)
+ Khoảng cách từ điểm A đến đường thẳng ( d ’ ) là :
d( A; d’) =
= 2
Chuyên đề Toán 10 : khá không thiếu triết lý và các dạng bài tập có đáp án khác :
Giới thiệu kênh Youtube Tôi
Xem thêm : Khoảng cách từ 1 điểm đến Ox lớp 10
Trang trước Trang sau
Video liên quan
Source: https://dichvusuachua24h.com
Category : Du Lịch
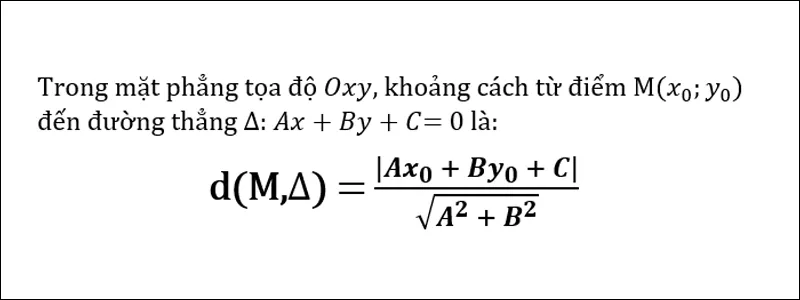



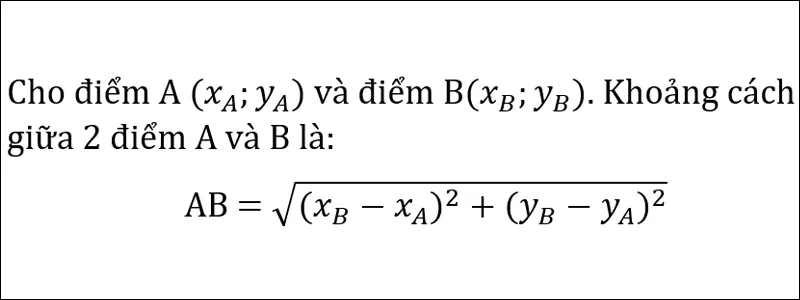
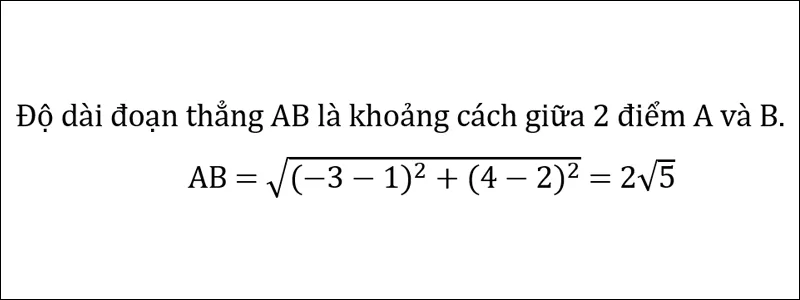











![\[ax + by + c = 0\]](https://cdn.giaibainhanh.com/cong-thuc-tinh-khoang-cach-tu-diem-den-duong-thang-trong-khong-gian--779b1282a003a46cf6bdb3f25f3c753f.wepb)
![\[d({M_0},\Delta ) = \frac{{\left[ {a{x_0} + b{y_0} + c} \right]}}{{\sqrt {{a^2} + {b^2}} }}\]](https://cdn.giaibainhanh.com/cong-thuc-tinh-khoang-cach-tu-diem-den-duong-thang-trong-khong-gian--53834c5d6bf61b8ad29144364f70dce1.wepb)