Cách tính khoảng cách từ 1 điểm đến 1 đường thẳng trong không gian Oxyz – Mathsilo
1. Phương pháp tính khoảng cách từ 1 điểm tới 1 đường thẳng trong không gian Oxyz
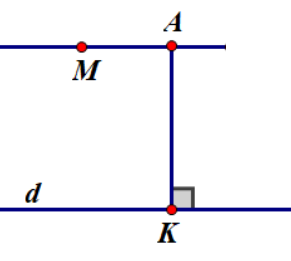
Bài toán : Giả sử có một điểm M không thuộc đường thẳng d. Hãy tính khoảng cách từ M tới d .
a. Phương pháp dựng hình
Phương pháp này đã được học từ lớp 11, nội dung cách tính như sau
Các bước triển khai :
- Bước 1. Trong mặt phẳng ( M, d) hạ MH ⊥ d với H ∈ d.
- Bước 2. Thực hiện việc xác định độ dài MH dựa trên hệ thức lượng trong tam giác, tứ giác, đường tròn, …
Chú ý :
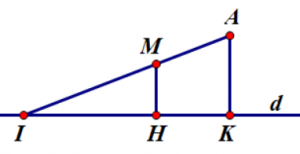
- Nếu tồn tại đường thẳng a qua A và song song với d thì: d(M,d) = d(A,d) = AK với A∈ d.
- Nếu MA ∩ d = I, thì: $\frac{{d\left( {M,d} \right)}}{{d\left( {A,d} \right)}} = \frac{{MI}}{{AI}}$
b) Phương pháp tọa độ
Phương pháp 1
Cho điểm M và đường thẳng d ( có phương trình tham số hoặc chính tắc ) .
- Bước 1. Chọn điểm A ∈ d
- Bước 2. Tìm vecto chỉ phương $\overrightarrow {{u_d}} $ của đường thẳng d
- Bước 3: Áp dụng công thức $d\left( {M,d} \right) = \frac{{\left[ {\overrightarrow {{u_d}} ,\overrightarrow {AM} } \right]}}{{\left| {\overrightarrow {{u_d}} } \right|}}$
Phương pháp 2
Gọi N ( x, y, x ) ∈ d. Tính MN2 theo t ( t là tham số trong phương trình đường thẳng d )
- Tìm t để MN2 nhỏ nhất
- Khi đó N ≡ H. Do đó d( M, d) = MH
2. Bài tập
Bài tập 1. Trong mặt phẳng Oxy cho đường thẳng $\Delta$ và đường thẳng a lần lượt có phương trình là: $2x+3y-1=0$ và $4x+3y-5=0$
a. Tính khoảng cách từ điểm USD M ( 2 ; 1 ) USD đến đường thẳng $ \ Delta $
b. Tính khoảng cách từ điểm $ A ( 2 ; 4 ) USD đến đường thẳng USD a USD
Giải
a. Khoảng cách từ điểm USD M ( 2 ; 1 ) USD đến đường thẳng $ \ Delta $ là :
USD d ( M, \ Delta ) = \ dfrac { | 2.2 + 3.1 – 1 | } { \ sqrt { 2 ^ 2 + 3 ^ 2 } } $
=> $ d ( M, \ Delta ) = \ dfrac { 6 } { \ sqrt { 13 } } $
=> $ d ( M, \ Delta ) = \ dfrac { 6 \ sqrt { 13 } } { 13 } $
b. Khoảng cách từ điểm $ A ( 2 ; 4 ) USD đến đường thẳng $ a $ là :
USD d ( M, a ) = \ dfrac { | 4.2 + 3.4 – 5 | } { \ sqrt { 4 ^ 2 + 3 ^ 2 } } $
=> $ d ( M, a ) = \ dfrac { 15 } { \ sqrt { 4 ^ 2 + 3 ^ 2 } } $
=> $ d ( M, a ) = \ dfrac { 15 } { 5 } = 3 USDBài tập 2: Cho tam giác ABC biết $A(1;2)$; $B(2;3)$; $C(-1;2)$. Tính độ dài đường cao xuất phát từ đỉnh A xuống cạnh BC.
Giải
Độ dài đường cao xuất phát từ đỉnh A đến cạnh BC chính là khoảng cách từ điểm A đến đường thẳng BC. Do đó ta cần viết được phương trình của đường thẳng BC .
Ta có : $ \ vec { BC } = ( – 3 ; – 1 ) USD
Vectơ pháp tuyến của đường thẳng BC là : $ \ vec { n } _ { BC } = ( 1 ; – 3 ) USDĐường thẳng BC đi qua điểm $B(2;3)$ có phương trình là:
USD 1. ( x-2 ) – 3 ( y-3 ) = 0 $ < => $ x-3y+7 = 0 USD
Khoảng cách từ điểm $ A ( 1 ; 2 ) USD đến đường thẳng BC là :
USD d ( A, BC ) = \ dfrac { | 1-3. 2 + 7 | } { \ sqrt { 1 ^ 2 + ( – 3 ) ^ 2 } } $
=> $ d ( A, BC ) = \ dfrac { 2 } { \ sqrt { 10 } } $
=> $ d ( A, BC ) = \ dfrac { \ sqrt { 10 } } { 5 } $
Vậy độ dài đường cao xuất phát từ đỉnh A đến cạnh BC bằng : $ \ dfrac { \ sqrt { 10 } } { 5 } $Bài tập 3: Tìm tất cả những điểm nằm trên đường thẳng a có phương trình: $x+y-3=0$ và có khoảng cách đến đường thẳng b có phương trình $3x-4y+5=0$ bằng 3.
Hướng dẫn
Gọi USD M $ là điểm bất kỳ thuộc đường thẳng a. Khi đó ta có tọa độ của điểm USD M $ là : USD M ( x_M ; – x_M + 3 ) USD
Khoảng cách từ điểm M đến đường thẳng b là :
USD d ( M, b ) = \ dfrac { | 3 x_M – 4 ( x_M + 3 ) + 5 | } { \ sqrt { 3 ^ 2 + ( – 4 ) ^ 2 } } $
=> $ d ( M, b ) = \ dfrac { | – x_M-7 | } { 5 } $
=> $ d ( M, b ) = \ dfrac { | x_M + 7 | } { 5 } $
Theo bài ra khoảng cách từ điểm M đến đường thẳng b bằng 3 nên ta có :
USD \ dfrac { | x_M + 7 | } { 5 } = 3 USD<=> $|x_M+7|=15$
<=> $x_M+7=15$ hoặc $x_M+7=-15$
<=> $x_M=8$ hoặc $x_M=-19$
Vậy có hai điểm M thuộc đường thẳng a và có khoảng cách đến đường thẳng b bằng 3 là hai điểm $ M_1 ( 8 ; – 5 ) USD và $ M_2 ( – 22 ; – 19 ) USD
Bài tập rèn luyện tính khoảng cách từ một điểm tới một đường thẳng
Bài tập 1: trong mặt phẳng Oxy cho đường thẳng a và b lần lượt có phương trình là: $2x-3y+7=0$ và $4x+3y-11=0$.
a. Tính khoảng cách từ điểm $ A ( 2 ; – 3 ) USD tới đường thẳng a
b. Tính khoảng cách từ điểm $ B ( – 4 ; 3 ) USD tới đường thẳng bBài tập 2: Tính diện tích hình vuông có toạ độ một đỉnh là A(4;2) và phương trình một đường chéo là $x+2y+2=0$
Bài tập 3: Viết phương trình của đường thẳng a song song với đường thẳng b: 3x + 4y – 1 = 0 và cách đường thẳng b một đoạn bằng 2
Bài tập 4: Tìm bán kính của đường tròn tâm I(2, –3) và tiếp xúc với đường thẳng: 12x -5y +3 = 0
Trên đây là bài viết san sẻ về cách tính khoảng cách từ 1 điểm đến 1 đường thẳng trong khoảng trống hệ tọa độ oxyz. Hy vọng rằng bài viết này đã giúp ích được cho bạn .
Source: https://dichvusuachua24h.com
Category : Du Lịch