1. Bài toán tính khoảng cách từ một điểm đến một đường thẳng

Phương pháp:

Để tính khoảng cách từ điểm $M$ đến đường thẳng $\Delta $ ta cần xác định được hình chiếu $H$ của điểm $M$ trên đường thẳng $\Delta $, rồi xem $MH$ là đường cao của một tam giác nào đó để tính.

Bạn đang đọc: Các dạng toán về khoảng cách – https://dichvusuachua24h.com

Điểm $ H $ thường được dựng theo hai cách sau :

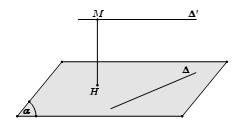
Cách 1: Trong $mp\left( {M,\Delta } \right)$ vẽ $MH \bot \Delta  \Rightarrow d\left( {M,\Delta } \right) = MH$

Cách 2: Dựng mặt phẳng $\left( \alpha  \right)$ qua $M$ và vuông góc với $\Delta $ tại $H$.

Khi đó USD d \ left ( { M, \ Delta } \ right ) = MH $ .Hai công thức sau thường được dùng để tính $ MH $
CT1 : USD \ Delta MAB $ vuông tại USD M $ và có đường cao $ MH $ thì $ \ dfrac { 1 } { { M { H ^ 2 } } } = \ dfrac { 1 } { { M { A ^ 2 } } } + \ dfrac { 1 } { { M { B ^ 2 } } } $ .
CT2 : $ MH $ là đường cao của USD \ Delta MAB $ thì $ MH = \ dfrac { { 2 { S_ { MAB } } } } { { AB } } $ .

2. Tính khoảng cách từ một điểm đến một mặt phẳng

Phương pháp:

Để tính được khoảng từ điểm USD M $ đến mặt phẳng $ \ left ( \ alpha \ right ) USD thì điều quan trọng nhất là ta phải xác lập được hình chiếu của điểm USD M $ trên $ \ left ( \ alpha \ right ) USD .

TH1:

– Dựng \ ( AK \ bot \ Delta \ Rightarrow \ Delta \ bot \ left ( { SAK } \ right ) \ Rightarrow \ left ( \ alpha \ right ) \ bot \ left ( { SAK } \ right ) \ ) và \ ( \ left ( \ alpha \ right ) \ cap \ left ( { SAK } \ right ) = SK \ ) .- Dựng \ ( AH \ bot SK \ Rightarrow AH \ bot \ left ( \ alpha \ right ) \ Rightarrow d \ left ( { A, \ left ( \ alpha \ right ) } \ right ) = AH \ )

TH2:

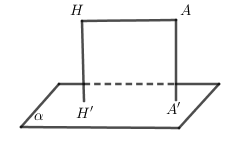– Tìm điểm \ ( H \ in \ left ( \ alpha \ right ) \ ) sao cho \ ( AH / / \ left ( \ alpha \ right ) \ Rightarrow d \ left ( { A, \ left ( \ alpha \ right ) } \ right ) = d \ left ( { H, \ left ( \ alpha \ right ) } \ right ) \ )

TH3:

– Tìm điểm \ ( H \ ) sao cho \ ( AH \ cap \ left ( \ alpha \ right ) = I \ )

– Khi đó : \ ( \ dfrac { { d \ left ( { A, \ left ( \ alpha \ right ) } \ right ) } } { { d \ left ( { H, \ left ( \ alpha \ right ) } \ right ) } } = \ dfrac { { IA } } { { IH } } \ Rightarrow { \ rm { } } d \ left ( { A, \ left ( \ alpha \ right ) } \ right ) = \ dfrac { { IA } } { { IH } }. d \ left ( { H, \ left ( \ alpha \ right ) } \ right ) { \ rm { } } \ )Một tác dụng có nhiều ứng dụng để tính khoảng cách từ một điểm đến mặt phẳng so với tứ diện vuông ( tương tư như hệ thức lượng trong tam giác vuông ) là :Nếu tứ diện $ OABC $ có $ OA, OB, OC $ đôi một vuông góc và có đường cao $ OH $ thì $ \ dfrac { 1 } { { O { H ^ 2 } } } = \ dfrac { 1 } { { O { A ^ 2 } } } + \ dfrac { 1 } { { O { B ^ 2 } } } + \ dfrac { 1 } { { O { C ^ 2 } } } $ .

3. Phương pháp tính khoảng cách giữa hai đường thẳng

Phương pháp:

Xem thêm: So sánh ẩm thực Trung Quốc và Việt Nam

Để tính khoảng cách giữa hai đường thẳng chéo nhau ta hoàn toàn có thể dùng một trong các cách sau :

+) Phương pháp 1: Dựng đoạn vuông góc chung $MN$ của $a$ và $b$, khi đó $d\left( {a,b} \right) = MN$.

Một số trường hợp hay gặp khi dựng đoạn vuông góc chung của hai đường thẳng chéo nhau :

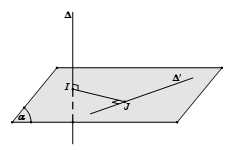
Trường hợp 1: $\Delta $ và $\Delta ‘$ vừa chéo nhau vừa vuông góc với nhau

– Bước 1: Chọn mặt phẳng $(\alpha )$ chứa $\Delta ‘$ và vuông góc với $\Delta $ tại $I$.

– Bước 2: Trong mặt phẳng $(\alpha )$ kẻ $IJ \bot \Delta ‘$.

Khi đó $ IJ $ là đoạn vuông góc chung và USD d ( \ Delta, \ Delta ‘ ) = IJ $ .

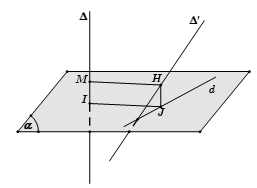
Trường hợp 2: $\Delta $ và $\Delta ‘$ chéo nhau mà không vuông góc với nhau

– Bước 1: Chọn mặt phẳng $(\alpha )$ chứa $\Delta ‘$ và song song với $\Delta $.

– Bước 2: Dựng $d$ là hình chiếu vuông góc của $\Delta $ xuống $(\alpha )$ bằng cách lấy điểm $M \in \Delta $ dựng đoạn $MN \bot \left( \alpha  \right)$, lúc đó $d$ là đường thẳng đi qua $N$ và song song với $\Delta $.

– Bước 3: Gọi $H = d \cap \Delta ‘$, dựng $HK//MN$

Khi đó $ HK $ là đoạn vuông góc chung và USD d ( \ Delta, \ Delta ‘ ) = HK = MN $ .

Hoặc

– Bước 1: Chọn mặt phẳng $(\alpha ) \bot \Delta $ tại $I$.

– Bước 2: Tìm hình chiếu $d$ của $\Delta ‘$ xuống mặt phẳng $(\alpha )$.

– Bước 3: Trong mặt phẳng $(\alpha )$, dựng $IJ \bot d$, từ $J$ dựng đường thẳng song song với $\Delta $ cắt $\Delta ‘$ tại $H$, từ $H$ dựng $HM//IJ$.

Khi đó $ HM $ là đoạn vuông góc chung và USD d ( \ Delta, \ Delta ‘ ) = HM = IJ $ .

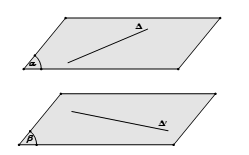
+) Phương pháp 2: Chọn mặt phẳng $(\alpha )$ chứa đường thẳng $\Delta $ và song song với $\Delta ‘$. Khi đó $d(\Delta ,\Delta ‘) = d(\Delta ‘,(\alpha ))$

+) Phương pháp 3: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.

+) Phương pháp 4: Sử dụng phương pháp vec tơ

Xem thêm: Buffet là gì? Phân loại, cách ăn buffet đúng cách, lâu no mà vẫn lịch sự

a ) $ MN $ là đoạn vuông góc chung của $ AB $ và $ CD $ khi và chỉ khi $ \ left \ { \ begin { array } { l } \ overrightarrow { AM } = x \ overrightarrow { AB } \ \ \ overrightarrow { CN } = y \ overrightarrow { CD } \ \ \ overrightarrow { MN }. \ overrightarrow { AB } = 0 \ \ \ overrightarrow { MN }. \ overrightarrow { CD } = 0 \ end { array } \ right. $b ) Nếu trong $ \ left ( \ alpha \ right ) USD có hai vec tơ không cùng phương $ \ overrightarrow { { u_1 } }, \ overrightarrow { { u_2 } } $ thì $ OH = d \ left ( { O, \ left ( \ alpha \ right ) } \ right ) \ Leftrightarrow \ left \ { \ begin { array } { l } \ overrightarrow { OH } \ bot \ overrightarrow { { u_1 } } \ \ \ overrightarrow { OH } \ bot \ overrightarrow { { u_2 } } \ \ H \ in \ left ( \ alpha \ right ) \ end { array } \ right. \ Leftrightarrow \ left \ { \ begin { array } { l } \ overrightarrow { OH }. \ overrightarrow { { u_1 } } = 0 \ \ \ overrightarrow { OH }. \ overrightarrow { { u_2 } } = 0 \ \ H \ in \ left ( \ alpha \ right ) \ end { array } \ right. $

Source: https://dichvusuachua24h.com
Category : Du Lịch