Hướng dẫn chi tiết cách tính khoảng cách từ một điểm đến một đường thẳng
1. Thế nào là khoảng cách từ một điểm đến một đường thẳng?
Để tính được khoảng cách của một điểm đến một đường thẳng thì thứ nhất tất cả chúng ta tìm hiểu và khám phá xem khoảng cách từ điểm đến đường thẳng trong khoảng trống là gì ?
Trong khoảng trống cho điểm M và đường thẳng Δ bất kể và H là hình chiếu của điểm M lên đường thẳng Δ. Khi đó, khoảng cách từ điểm M đến đường thẳng Δ là khoảng cách giữa hai điểm M và H ( độ dài đoạn thẳng MH ). Hay nói cách khác khoảng cách giữa điểm và đường thẳng chính là khoảng cách giữa điểm và hình chiếu của nó trên đường thẳng .Kí hiệu: d(M,Δ) = MH trong đó H là hình chiếu của M trên Δ.
2. Phương pháp tính khoảng cách từ một điểm đến một đường thẳng
2.1. Công thức
Phương pháp : Để tính khoảng cách từ điểm M đến đường thẳng Δ ta cần xác lập được hình chiếu H của điểm M trên đường thẳng Δ, rồi xem MH là đường cao của một tam giác nào đó để tính. Cách tính khoảng cách từ điểm M đến đường thẳng Δ d ( M, Δ ) như sau :
– Cho đường thẳng $ Δ : ax + by + c = 0 $ và điểm USD M ( x_0 ; y_0 ) USD. Khi đó khoảng cách từ điểm M đến đường thẳng Δ là : USD d ( M, \ Delta ) = \ frac { \ left | ax_0 + by_0 + c \ right | } { \ sqrt { a ^ 2 + b ^ 2 } } $
– Cho điểm $ A ( x_A ; y_A ) USD và điểm $ B ( x_B ; y_B ) USD. Khoảng cách hai điểm này là :
USD AB = \ sqrt { ( x_B-x_a ) ^ 2 + ( y_B-y_A ) ^ 2 } $2.2. Bài tập ví dụ tính khoảng cách từ một điểm đến một đường thẳng
Một số ví dụ để các em hoàn toàn có thể chớp lấy được giải pháp tính khoảng cách từ một điểm đến một đường thẳng :
VD1: Tìm khoảng cách từ điểm M(1; 2) đến đường thẳng $(D): 4x+3y-2=0$
Hướng dẫn giải:
Áp dụng công thức tính khoảng cách từ một điểm đến một đường thẳng ta có :
USD d ( M, D ) = \ frac { \ left | 4.1 + 3.2 – 2 \ right | } { \ sqrt { 4 ^ 2 + 3 ^ 2 } } = \ frac { 8 } { 5 } $VD2: Khoảng cách từ giao điểm của hai đường thẳng (a): x – 3y + 4 = 0 và
( b ) : 2 x + 3 y – 1 = 0 đến đường thẳng ∆ : 3 x + y + 16 = 0 bằng :
Hướng dẫn giải:
Gọi A là giao điểm của hai đường thẳng ( a ) và ( b ) tọa độ điểm A là nghiệm hệ phương trình :
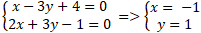
⇒ A ( – 1 ; 1 )
Khoảng cách từ điểm A đến đường thẳng ∆ là :
USD d ( M, D ) = \ frac { \ left | 3. ( – 1 ) + 1 + 16 \ right | } { \ sqrt { 3 ^ 2 + 1 ^ 2 } } = \ frac { 14 } { \ sqrt { 10 } } $VD3: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A(3; – 4); B(1; 5) và C(3;1). Tính diện tích tam giác ABC.
Hướng dẫn giải:
Ta có phương trình đường thẳng BC :
⇒ Phương trình BC : USD 2 ( x-1 ) + 1 ( y-5 ) = 0 $ hay USD 2 x + y-7 = 0 USD
⇒ $ d ( A, BC ) = \ frac { \ left | 2.3 + ( – 4 ) – 7 \ right | } { \ sqrt { 2 ^ 2 + 1 ^ 2 } } = \ frac { 5 } { \ sqrt { 5 } } = \ sqrt { 5 } $
USD BC = \ sqrt { ( 3-1 ) ^ 2 + ( 1/5 ) ^ 2 } = 2 \ sqrt { 5 } $
⇒ Diện tích tam giác ABC là : USD S = \ frac { 1 } { 2 }. d ( A ; BC ). BC = 12. 5.25 = 5 USD
3. Bài tập luyện tập tính khoảng cách từ một điểm đến một đường thẳng
Câu 1: Khoảng cách từ điểm M(1; -1) đến đường thẳng $(a): 3x – 4y – 21 = 0$ là:
A. 1 B. 2 C. 45 D. 145
Câu 2: Khoảng cách từ điểm O đến đường thẳng $d:\frac{x}{6}+\frac{y}{8}=1$ là:
A. 4,8 B. 110 C. 1 D. 6
Câu 3: Khoảng cách từ điểm M(2; 0) đến đường thẳng
là:
A. 2 B. $ \ frac { 2 } { 5 } $ C. $ \ frac { 10 } { { \ sqrt { 5 } } } $ D. $ \ frac { \ sqrt { 5 } } { 2 } $
Câu 4: Đường tròn (C) có tâm là gốc tọa độ O(0; 0) và tiếp xúc với đường thẳng
USD ( d ) : 8 x + 6 y + 100 = 0 USD. Bán kính R của đường tròn ( C ) bằng :
A. R = 4 B. R = 6 C. R = 8 D. R = 10Câu 5: Khoảng cách từ điểm M( -1; 1) đến đường thẳng d: 3x – 4y + 5 = 0 bằng:
A. $ \ frac { 2 } { 5 } USD B. 1 C. $ \ frac { 4 } { 5 } $ D. $ \ frac { 4 } { 25 } $
Câu 6: Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC có A( 1; 2) ; B(0; 3) và C(4; 0). Chiều cao của tam giác kẻ từ đỉnh A bằng:
A.. $ \ frac { 1 } { 5 } $ B. 3 C.. $ \ frac { 1 } { 25 } USD D.. $ \ frac { 3 } { 5 } $
Câu 7: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng $d_1: 4x-3y+5=0$ và $d_2: 3x+4y–5=0$, đỉnh A( 2; 1). Diện tích của hình chữ nhật là:
A. 1. B. 2 C. 3 D. 4
Câu 8: Khoảng cách từ điểm M( 2;0) đến đường thẳng
là:
A. 2 B. 25 C. 105 D. 52
Câu 9: Đường tròn ( C) có tâm I ( -2; -2) và tiếp xúc với đường thẳng
d : 5 x + 12 y – 10 = 0. Bán kính R của đường tròn ( C ) bằng :
A. R = $ \ frac { 44 } { 13 } $ B. R =. $ \ frac { 24 } { 13 } $ C. R = 44 D. R =. $ \ frac { 7 } { 13 } $Câu 10: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng (a) : 4x – 3y + 5 = 0 và (b) : 3x + 4y – 5 = 0. Biết hình chữ nhật có đỉnh A( 2 ;1). Diện tích của hình chữ nhật là:
A. 1 B. 2 C. 3 D. 4
Câu 11: Cho hai điểm A( 2; -1) và B( 0; 100) ; C( 2; -4).Tính diện tích tam giác ABC?
A. 3 B. 32 C. $ \ frac { 3 } { \ sqrt { 2 } } $ D. 147
Câu 12: Khoảng cách từ A(3; 1) đến đường thẳng
gần với số nào sau đây ?
Xem thêm: Ẩm thực Nhật Bản – Wikipedia tiếng Việt
A. 0,85 B. 0,9 C. 0,95 D. 1
Câu 13: Hai cạnh của hình chữ nhật nằm trên hai đường thẳng 4x – 3y + 5 = 0 và
3 x + 4 y + 5 = 0 đỉnh A ( 2 ; 1 ). Diện tích của hình chữ nhật là
A. 6 B. 2 C. 3 D. 4Câu 14: Tính diện tích hình bình hành ABCD biết A( 1; -2) ; B( 2; 0) và D( -1; 3)
A. 6 B. 4,5 C. 3 D. 9
Câu 15: Tính khoảng cách từ giao điểm của hai đường thẳng (d) : x + y – 2 = 0 và
( ∆ ) : 2 x + 3 y – 5 = 0 đến đường thẳng ( d ’ ) : 3 x – 4 y + 11 = 0
A. 1 B. 2 C. 3 D. 4Câu 16: Cho một đường thẳng có phương trình có dạng Δ: – x + 3y + 1 = 0. Hãy tính khoảng cách từ điểm Q (2; 1) tới đường thẳng Δ.
A. $ \ sqrt { 10 } $ B. $ \ frac { 5 } { \ sqrt { 10 } } $ C. $ \ frac { \ sqrt { 10 } } { 5 } $ D. 5
Câu 17: Khoảng cách từ điểm P(1; 1) đến đường thẳng Δ:
A. 8,8 B. 6,8 C. 7 D. 8,6
Câu 18: Khoảng cách từ điểm P(1; 3) đến đường thẳng Δ:
A. 2 B. 2,5 C. 2,77 D. 3
Câu 19: Trong mặt phẳng Oxy cho đường thẳng Δ có phương trình: 2x + 3y -1 = 0. Tính khoảng cách điểm M(2; 1) đến đường thẳng Δ.
A. $ \ frac { \ sqrt { 13 } } { 13 } $ B. $ \ frac { 6 \ sqrt { 13 } } { 13 } $ C. $ \ frac { \ sqrt { 6 } } { 13 } $ D. $ \ frac { \ sqrt { 13 } } { 6 } $
Câu 20: Trong mặt phẳng Oxy cho đường thẳng a có phương trình: 4x + 3y – 5 = 0. Tính khoảng cách điểm A(2; 4) đến đường thẳng a.
A. $ \ frac { \ sqrt { 3 } } { 3 } $ B. $ \ frac { 1 } { 3 } $ C. 3 D. $ \ frac { 2 } { 3 } $
Đáp án :
1 2 3 4 5 6 7 8 9 10 D A A D A A B A A B 11 12 13 14 15 16 17 18 19 20 A B A D B C D C B
C
Bài viết trên đây đã tổng hợp hàng loạt công thức kim chỉ nan và cách vận dụng giải các bài tập tính khoảng cách từ một điểm đến một đường thẳng. Hy vọng rằng tài liệu trên sẽ là nguồn tìm hiểu thêm có ích cho các bạn học viên ôn tập thật tốt và đạt được nhiều điểm trên cao. Để đọc và học thêm nhiều kỹ năng và kiến thức mê hoặc về Toán lớp 10, Toán trung học phổ thông, Ôn thi THPT Quốc gia sớm cho 2 k6, … các em truy vấn trang web vuihoc.vn hoặc ĐK khóa học với các thầy cô VUIHOC ngay tại đây nhé !
Source: https://dichvusuachua24h.com
Category : Du Lịch























