Tính khoảng cách từ một điểm đến mặt phẳng bằng phương pháp trực tiếp
Mời các quý thầy cô và các em học viên cùng tìm hiểu thêm và tải về chi tiết cụ thể tài liệu dưới đây
Tính khoảng cách từ một điểm đến mặt phẳng bằng phương pháp trực tiếp
Dạng 1: d (H;(SAB)) = HK
Dạng 2: d (A;(SHB)) = AK
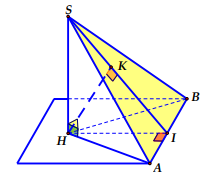
Bài 1. Cho hình chóp S ABC. có đáy ABC là tam giác vuông tại B, BAC = 600 ; SA = AC = a và vuông góc với đáy.
a ) Tính khoảng cách từ điểm A đến mặt phẳng SBC .
b ) Tính khoảng cách từ điểm B đến mặt phẳng SAC .Lời giải
a ) Trong tam giác vuông ABC, ta có
AB = AC.cosBAC = \ [ \ frac { a } { 2 } \ ]
Kẻ AH \ [ \ bot \ ] SB ( H \ [ \ in \ ] SB ). 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BC \ bot AB } \ \ { BC \ bot SA } \ end { array } } \ right. \ Rightarrow BC \ bot SAB \ Rightarrow BC \ bot AH \ ] 2
Từ 1 và 2, suy ra AH \ [ \ bot \ ] SBC. DO đó
d ( A, ( SBC ) ) = AH .
Trong tam giác vuông SAB, ta có
AH = \ [ \ frac { { SA.AB } } { { \ sqrt { S { A ^ 2 } + A { B ^ 2 } } } } = \ frac { { a \ sqrt 5 } } { 5 } \ ]
Vậy d ( A, ( SBC ) ) = AH = \ [ \ frac { { a \ sqrt 5 } } { 5 } \ ]
b ) Kẻ BK \ [ \ bot \ ] AC ( K \ [ \ in \ ] AC ) .
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BK \ bot AC } \ \ { BK \ bot SA } \ end { array } } \ right. \ Rightarrow BK \ bot SAC \ ] .
Do đó d ( B, ( SAC ) ) = BK
Trong tam giác vuông ABC, ta có BC = AC. sin BAC = \ [ \ frac { { a \ sqrt 3 } } { 2 } \ ] suy ra
BK = \ [ \ frac { { AB.BC } } { { \ sqrt { A { B ^ 2 } + B { C ^ 2 } } } } = \ frac { { a \ sqrt 3 } } { 4 } \ ]
Vậy d ( B ; ( SAC ) ) = \ [ \ frac { { a \ sqrt 3 } } { 4 } \ ]Bài 2. Cho hình chóp S ABC. có đáy ABC là tam giác vuông tại A, SA a và vuông góc với đáy, tam giác SBC cân tại S và tạo với đáy một góc 450. Tính khoảng cách từ điểm A đến mặt phẳng SBC .
Lời giải
Tam giác SBC cân tại S nên SB = SC .
Suy ra \ [ \ Delta \ ] SAB = \ [ \ Delta \ ] SAC ( cạnh huyền – cạnh góc vuông ) .
Do đó AB = AC. Vậy tam giác ABC vuông cân tại A .
Gọi E là trung điểm BC, suy ra AE \ [ \ bot \ ] BC .
Gọi K là hình chiếu của A trên SE, suy ra AK \ [ \ bot \ ] SE. 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BC \ bot AE } \ \ { BC \ bot SA } \ end { array } } \ right. \ Rightarrow BC \ bot SAE \ Rightarrow BC \ bot AK \ ] 2
Từ 1 và 2, suy ra AK \ [ \ bot \ ] ( SBC ) nên d ( A, ( SBC ) ) = AK .
Ta có : \ [ \ left. { \ begin { array } { * { 20 } { c } } { ( SBC ) \ cap ( ABC ) = BC } \ \ { SE \ subset ( SBC ), SE \ bot BC } \ \ { AE \ subset ( ABC ), AE \ bot BC } \ end { array } } \ right \ } \ ]
\ [ \ Rightarrow \ widehat { ( ( SBC ), ( ABC ) } ) = \ widehat { ( SE, AE ) } = \ widehat { SEA } = { 45 ^ 0 } \ ]
Tam gác SAE vuông tại A có \ [ \ widehat { SEA } = { 45 ^ 0 } \ ] nên là tam giác vuông cân, suy ra
AK = \ [ \ frac { { SE } } { 2 } = \ frac { { SA \ sqrt 2 } } { 2 } = \ frac { { a \ sqrt 2 } } { 2 } \ ]
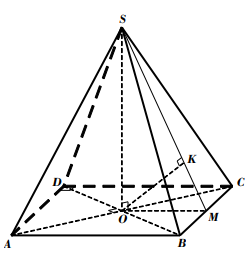
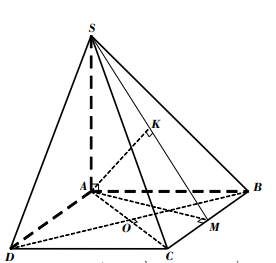
Vậy d ( A ; ( SBC ) ) = AK = \ [ \ frac { { a \ sqrt 2 } } { 2 } \ ] .Bài 3. Cho hình chóp S ABCD. có đáy ABCD là hình vuông tâm O, cạnh a ; SA = SB = SC = SD =\[a\sqrt 2 \]. Tính khoảng cách từ điểm O đến mặt phẳng (SBC) .
Lời giải
Do O là tâm hình vuông vắn nên OA = OB = OC = OD .
Mà SA = SB = SC = SD, suy ra SO là trục của đường tròn ngoại tiếp hình vuông vắn ABCD nên SO \ [ \ bot \ ] ( ABCD ) .
Trong tam giác vuông SOA ,
ta có SO = \ [ \ sqrt { S { A ^ 2 } – O { A ^ 2 } } = \ frac { { a \ sqrt 6 } } { 2 } \ ] .
Gọi M là trung điểm của BC, suy ra OM = \ [ \ frac { a } { 2 } \ ] vao OM \ [ \ bot \ ] BC .
Gọi K là hình chiếu của O trên SM, suy ra OK \ [ \ bot \ ] SM. 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BC \ bot OM } \ \ { BC \ bot SO } \ end { array } } \ right. \ Rightarrow BC \ bot SOM \ Rightarrow BC \ bot OK \ ] 2
Trong tam giác vuông SOM ,
ta có : \ [ \ frac { { SO.OM } } { { \ sqrt { S { O ^ 2 } + O { M ^ 2 } } } } = \ frac { { a \ sqrt { 42 } } } { { 14 } } \ ]
Vậy d ( O ; ( SBC ) ) = OK = \ [ \ frac { { a \ sqrt { 42 } } } { { 14 } } \ ]Bài 4. Cho hình chóp S ABCD có đáy ABCD là hình thang vuông tại A và B, AB = BC = a, AD = 2a. Cạnh bên SA = a và vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng SCD .
Lời giải
a ) Gọi M là trung điểm AD, suy ra ABCM là hình vuông vắn .
Do đó CM = MA = \ [ \ frac { { AD } } { 2 } \ ] nên tam gác ACD vuông tại C .
Kẻ AK \ [ \ bot \ ] SC, ( K \ [ \ in \ ] SC ) 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { CD \ bot AC } \ \ { CD \ bot SA } \ end { array } } \ right. \ Rightarrow CD \ bot SAC \ Rightarrow CD \ bot AK \ ] 2
Từ 1 và 2, suy ra AK \ [ \ bot \ ] ( SAC ) nên d ( A, ( SCD ) ) = AK .
Trong tam giác vuông SAC, ta có
AK = \ [ \ frac { { SA.AC } } { { \ sqrt { S { A ^ 2 } + A { C ^ 2 } } } } \ frac { { a. a \ sqrt 2 } } { { \ sqrt { { a ^ 2 } + 2 { a ^ 2 } } } } = \ frac { { a \ sqrt 6 } } { 3 } \ ]
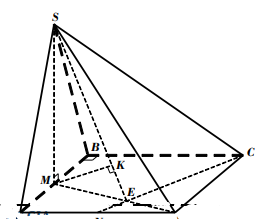
Vậy d ( A, ( SCD ) ) = AK = \ [ \ frac { { a \ sqrt 6 } } { 3 } \ ]Bài 5. Cho hình chóp S ABCD. có đáy ABCD là hình thoi cạnh a ,góc BAD = 1200 ; cạnh bên SA vuông góc với đáy. Gọi M là trung điểm cạnh BC. Tính khoảng cách từ điểm A đến mặt phẳng SBC, biết góc SMA = 450.
Lời giải
Do góc BAD = 1200 suy ra góc ABC = 600 nên tam giác ABC đều cạnh a .
Suy ra AM là đường cao trong tam giác đều ABC và AM = \ [ \ frac { { a \ sqrt 3 } } { 2 } \ ]
Kẻ AK \ [ \ bot \ ] SM ( K \ [ \ in \ ] SM ) 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BC \ bot AM } \ \ { BC \ bot SA } \ end { array } } \ right. \ Rightarrow BC \ bot SAM \ Rightarrow BC \ bot AK \ ] 2
Từ 1 và 2, suy ra AK \ [ \ bot \ ] ( SBC ) nên d ( A, ( SBC ) ) = AK
Trong tam giác vuông AKM ,
ta có AK = AM. sin \ [ \ widehat { SMA } \ ] = \ [ \ frac { { a \ sqrt 6 } } { 4 } \ ]
Vậy d ( D ; ( SBC ) ) = d ( A, ( SBC ) ) = \ [ \ frac { { a \ sqrt 6 } } { 4 } \ ]Bài 6. Cho hình chóp S ABCD có đáy ABCD là hình vuông cạnh a, tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy. Gọi M, N lần lượt là trung điểm của AB, AD. Tính khoảng cách từ M đến mặt phẳng SCN .
Lời giải
Tam giác SAB đều và có M là trung điểm AB nên SM AB. Mà ( SAB ) \ [ \ bot \ ] ( ABCD ) theo giao tuyến AB nên SM \ [ \ bot \ ] ( ABCD ) .
Ta có \ [ \ Delta \ ] AMD = \ [ \ Delta \ ] DNC suy ra \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { \ widehat { AMD } = \ widehat { DNC } } \ \ { \ widehat { ADM } = \ widehat { DCN } } \ end { array } } \ right. \ ]
Mà \ [ \ widehat { ADM } + \ widehat { AMD } = { 90 ^ 0 } \ ]
suy ra \ [ \ widehat { ADM } + \ widehat { DNC } = { 90 ^ 0 } \ ] hay CN \ [ \ bot \ ] DM .
Gọi E = DM \ [ \ cap \ ] CN, K là hình chiếu vuông góc của M trên SE suy ra MK \ [ \ bot \ ] SE. 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { CN \ bot DM } \ \ { CN \ bot SM } \ end { array } } \ right. \ Rightarrow CN \ bot ( SMD ) \ Rightarrow CN \ bot MK \ ] 2
Từ 1 và 2 suy ra \ [ MK \ bot ( SCN ) \ ]. Do đó d ( M ; ( SCN ) ) = MK
Ta có SM = \ [ \ frac { { a \ sqrt 3 } } { 2 } \ ] ; DM = \ [ \ sqrt { A { D ^ 2 } + A { M ^ 2 } } \ ] = \ [ \ frac { { a \ sqrt 5 } } { 2 } \ ]
DE = \ [ \ frac { { DC.DN } } { { \ sqrt { D { C ^ 2 } + D { N ^ 2 } } } } \ ] = \ [ \ frac { { a \ sqrt 5 } } { 2 } \ ] .
Suy ra ME = MD – DE = \ [ \ frac { { 3 a \ sqrt 5 } } { { 10 } } \ ] .
Trong tam giác vuông SME ,
ta có MK = \ [ \ frac { { SM.SE } } { { \ sqrt { S { M ^ 2 } + S { E ^ 2 } } } } \ ] = \ [ \ frac { { 3 a \ sqrt 2 } } { 8 } \ ]
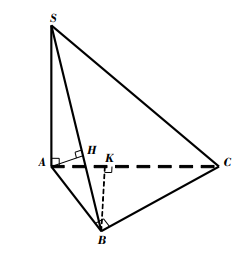
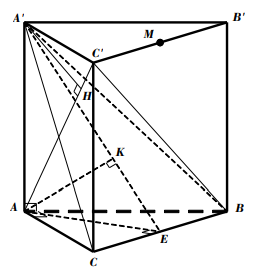
Vậy d ( M ; ( SCN ) ) = MK = \ [ \ frac { { 3 a \ sqrt 2 } } { 8 } \ ] .Bài 7. Cho lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông với AB = AC = a, góc giữa BC’ và mặt phẳng (ACC’A’) bằng 300. Gọi M là trung điểm của B’C’. Tính khoảng cách từ điểm A đến mặt phẳng (A’BC) .
Lời giải
Theo giả thiết tam giác ABC vuông cân tại A .
Vì \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BA \ bot AC } \ \ { B { \ rm { A } } \ bot { \ rm { A } } A ‘ } \ end { array } } \ right. \ Rightarrow BA \ bot ( ACC’A ‘ ) \ ] suy ra hình chiếu vuông góc của BC ‘ trên mặt phẳng ( ACC’A ’ ) là AC ‘ nên
300 = BC ; ACC’A ’ = BC ’ ; AC ’ = BC’A .
Trong tam giác vuông BAC ’, ta có
AC ’ = AB.cotBC ’ A = \ [ a \ sqrt 3 \ ]
Trong tam giác vuông AA’C ’, ta có
AA ’ = \ [ \ sqrt { AC { ‘ ^ 2 } + A ‘ { C ^ 2 } } \ ] = \ [ a \ sqrt 2 \ ]
a ) Gọi E là trung điểm của BC, suy ra AE \ [ \ bot \ ] BC .
Kẻ AK \ [ \ bot \ ] A’E ( K \ [ \ in \ ] A’E ). 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BC \ bot AE } \ \ { B { \ rm { C } } \ bot { \ rm { A } } A ‘ } \ end { array } } \ right. \ Rightarrow BC \ bot ( A’AE ) \ Rightarrow BC \ bot AK \ ] 2
Từ 1 và 2, suy ra AK \ [ \ bot \ ] ( A’BC ) nên d ( A, ( A’BC ) ) = AK
Trong tam giác vuông A’AE ,
ta có AE = \ [ \ frac { { a \ sqrt 2 } } { 2 } \ ] nên AK = \ [ \ frac { { AA ‘. AE } } { { \ sqrt { AA { ‘ ^ 2 } + A { E ^ 2 } } } } \ ] = \ [ \ frac { { a \ sqrt { 10 } } } { 5 } \ ]
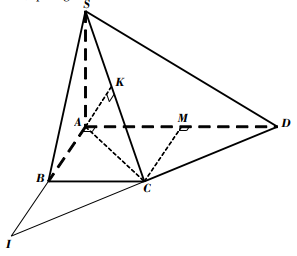
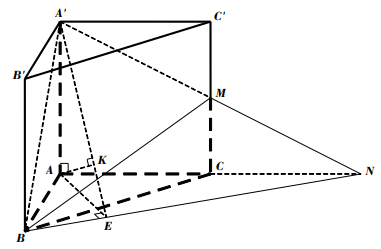
Vậy d ( A ; ( A’BC ) ) = AK = \ [ \ frac { { a \ sqrt { 10 } } } { 5 } \ ]Bài 8. Cho lăng trụ đứng ABC’A’B’C’ có đáy ABC là tam giác với AB = a, AC = 2a \[\widehat {BAC}\] = 1200 ; AA’ =\[2a\sqrt 5 \]. Gọi M là trung điểm CC’. Tính khoảng cách từ điểm A đến mặt phẳng (A’BM) .
Lời giải
Kéo dài AM ‘ cắt AC tại N .
Suy ra AN = 2AC = 4 a và d ( A, ( A’BM ) ) = d ( A, ( A’BN ) ) .
Gọi E là hình chiếu vuông góc của A trên BN, suy ra AE \ [ \ bot \ ] BN .
Kẻ AK \ [ \ bot \ ] A’E ( K \ [ \ in \ ] A’E ). 1
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BN \ bot AE } \ \ { BN \ bot { \ rm { A } } A ‘ } \ end { array } } \ right. \ Rightarrow BN \ bot ( A’AE ) \ Rightarrow BN \ bot AK \ ] 2
Từ 1 và 2, suy ra AK \ [ \ bot \ ] ( A’BN ) nên d ( A, ( A’BN ) ) = AK .
Áp dụng định lí hàm số côsin trong tam giác ABN, ta có
BN = \ [ \ sqrt { A { B ^ 2 } + A { N ^ 2 } – 2AB. AN. \ cos BAC } = a \ sqrt { 21 } \ ]
Ta có
S \ [ \ Delta ABN \ ] = \ [ \ frac { 1 } { 2 } AB.AN. \ sin BAC = \ frac { 1 } { 2 } BN.AE \ ]
\ [ \ Rightarrow AE = \ frac { { AB.AN. \ sin BAC } } { { BN } } = \ frac { { 2 a \ sqrt 7 } } { 7 } \ ]
Trong tam giác vuông A’AE ,
ta có AK = \ [ \ frac { { AA ‘. AE } } { { \ sqrt { AA { ‘ ^ 2 } + A { E ^ 2 } } } } = \ frac { { a \ sqrt 5 } } { 3 } \ ]
Vậy d ( A, ( A’BM ) ) = AK = \ [ \ frac { { a \ sqrt 5 } } { 3 } \ ]BÀI TẬP VỀ NHÀ
Bài 1. Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = \[a\sqrt 3 \] và vuông góc với đáy. Tính khoảng cách từ điểm A đến mặt phẳng SBC .
Lời giải
Kẻ AH \ [ \ bot \ ] SB ( H \ [ \ in \ ] SB ) .
Ta có \ [ \ left \ { { \ begin { array } { * { 20 } { c } } { BC \ bot AB } \ \ { BC \ bot S { \ rm { A } } } \ end { array } } \ right. \ Rightarrow BC \ bot ( SAB ) \ ]
\ [ \ Rightarrow BC \ bot AH \ Rightarrow AH \ bot ( SBC ) \ ]
Do đó d ( A, ( SBC ) ) = AH .Trong tam giác vuông SAB ,
ta có AH = \ [ \ frac { { SA.AB } } { { \ sqrt { S { A ^ 2 } + A { B ^ 2 } } } } = \ frac { { a \ sqrt 3 } } { 2 } \ ] .
Vậy d ( A, ( SBC ) ) = \ [ \ frac { { a \ sqrt 3 } } { 2 } \ ] .
Xem thêm
Source: https://dichvusuachua24h.com
Category : Du Lịch