Bài tập về Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song chọn lọc
Tài liệu Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song gồm các nội dung chính sau :
A. Lý thuyết
Bạn đang đọc: Bài tập về Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song chọn lọc
– tóm tắt triết lý ngắn gọn .
B. Bài tập tự luyện
– gồm 33 bài tập tự luyện giúp học viên tự rèn luyện cách giải các dạng Bài tập Khoảng cách từ một điểm đến đường thẳng, hai đường thẳng song song .
Mời các quý thầy cô và các em học viên cùng tìm hiểu thêm và tải về cụ thể tài liệu dưới đây :
KHOẢNG CÁCH TỪ MỘT ĐIỂM ĐẾN ĐƯỜNG THẲNG, HAI ĐƯỜNG THẲNG SONG SONG
A. LÝ THUYẾT
Khoảng cách:
• Khoảng cách từ điểm MxM ; yM đến Δ : Ax + By + C = 0 là :
MH = dM, Δ = AxM + ByM + CA2 + B2
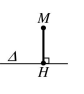
Chú ý: dM,Ox=yM,dM,Oy=xM
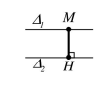
• Khoảng cách giữa hai đường thẳng Δ1 và Δ2
Nếu Δ1 và cắt hoặc trùng nhau thì d Δ1,Δ2=0
Xem thêm: Ẩm thực Nhật Bản – Wikipedia tiếng Việt
Nếu Δ1 / / Δ2 thì d Δ1, Δ2 = d M, Δ2 = MH với M ∈ Δ1
Chú ý:
Cho hai đường thẳng song song Δ1 và Δ2
Biết Δ1 : A1x + B1y + C1 = 0 và Δ2 : A2x + B2y + C2 = 0
Đường thẳng Δ3 song song và cách đều Δ1 và Δ2 có dạng :
Ax + By + C1 + C22 = 0
B. BÀI TẬP TỰ LUYỆN
Câu 1. Trong mặt phẳng với hệ tọa độ Oxy, cho điểm Mx0;y0 và đường thẳng Δ:ax+by+c=0. Khoảng cách từ điểm M đến Δ được tính bằng công thức:
A. dM,Δ= ax0+by0a2+b2. B. dM,Δ= ax0+by0a2+b2.
C. dM,Δ= ax0+by0+ca2+b2. D. dM,Δ= ax0+by0+ca2+b2.
Câu 2. Khoảng cách từ điểm M−1;1 đến đường thẳng Δ:3x−4y−3=0 bằng:
A. 25. B. 2. C. 45. D. 425.
Câu 3. Khoảng cách từ giao điểm của hai đường thẳng x−3y+4=0 và 2x+3y−1=0 đến đường thẳng Δ:3x+y+4=0 bằng:
A. 210. B. 3105. C. 105. D. 2 .
Xem thêm
Source: https://dichvusuachua24h.com
Category : Du Lịch